概要
- しきい値
 から超えた距離
から超えた距離 を最小化するように最適化を行う。
を最小化するように最適化を行う。
- svmではしきい値はgivenとするが、
 -svmでは、
-svmでは、 も最適化パラメータとする。このとき、
も最適化パラメータとする。このとき、 と
と がトレードオフの関係になる。ただし、ラグランジュ未定乗数法の式変形の仮定で消える。
がトレードオフの関係になる。ただし、ラグランジュ未定乗数法の式変形の仮定で消える。
 -svmは下記の最小化問題を解く。
-svmは下記の最小化問題を解く。
- [tex: C( \nu \epsilon + \frac{1}{N} \sum{n} (\eta_n + \hat{\eta}n)) + \frac{1}{2}|| w ||^2]
- これを式変形すると、式7.70が得られる。
- Relevance Vector Machine (RVM)はベイジアンなkernel method.
- 3章と同様に、事前分布のパラメータをiterativeに解く。
- SVMと比べ、予測時に使用する入力データの数が少なくなりやすい。
図7.8の再現
 -SVMでGaussianカーネルを用いる
-SVMでGaussianカーネルを用いる -insensitive tubeの定義が不明。
-insensitive tubeの定義が不明。  -SVMでは、
-SVMでは、 は0になるような・・・?
は0になるような・・・?
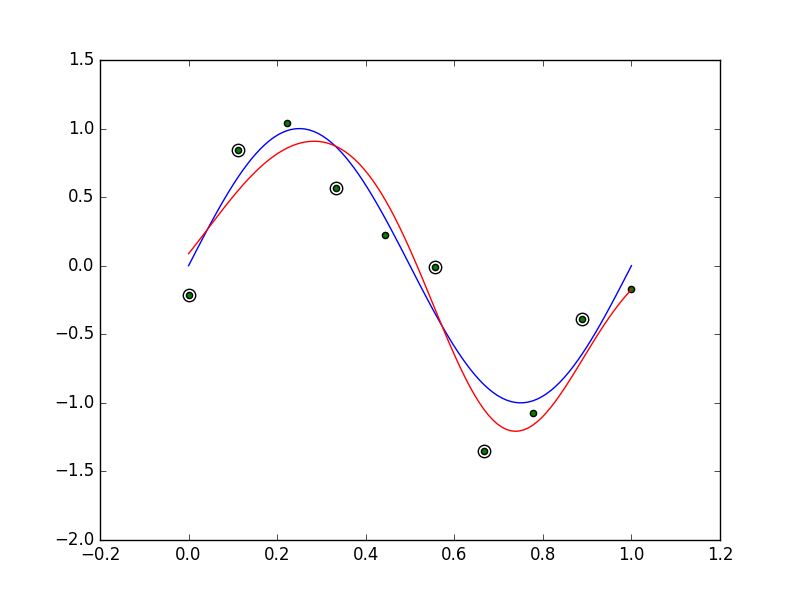
図7.9の再現
- Python初心者なので、まだまだ汚いです。そのうち修正する。
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
import math
class NuSvmRegression:
def __init__(self, nu, c, sigma):
self.nu = nu
self.c = c
self.sigma = sigma
self.x = None
self.t = None
self.b = None
self.d = None
def kernel(self, xn, xm):
return math.exp(- 0.5 * np.linalg.norm(xn - xm) ** 2 / (self.sigma ** 2))
def __call__(self, a):
n = a.shape[0] // 2
a0, a1 = a[0:n], a[n:2 * n]
d = (a0 - a1).flatten()
k = np.array([self.kernel(xn, xm) for xn in self.x for xm in self.x]).reshape(n, n)
v = - np.sum(d * self.t)
for i in range(n):
for j in range(n):
v += 0.5 * d[i] * d[j] * k[i][j]
return v
def learn(self, x, t):
self.x = x
self.t = t
n = x.shape[0]
initial_a = np.random.uniform(0, 1, n * 2)
cons = ({'type': 'ineq', 'fun': lambda a: a},
{'type': 'ineq', 'fun': lambda a: self.c / n - a},
{'type': 'ineq', 'fun': lambda a: self.nu * self.c - np.sum(a[0:n] + a[n:2 * n])},
{'type': 'eq', 'fun': lambda a: np.sum(a[0:n] - a[n:2 * n])})
res = minimize(self, initial_a, method='SLSQP', tol=1e-6, constraints=cons)
a = res.x
a0, a1 = a[0:n], a[n:2 * n]
d = (a0 - a1)
d = np.array([d0 if math.fabs(d0) > 1e-4 else 0 for d0 in d]).reshape(1, -1)
k = np.array([self.kernel(xn, xm) for xn in self.x for xm in self.x]).reshape(n, n)
self.b = np.average(t - np.dot(d, k))
self.d = d.flatten()
return res.x
def predict(self, x):
n = self.t.shape[0]
k = np.array([self.kernel(x, xm) for xm in self.x])
return np.sum(self.d * k) + self.b
class RvmRegression:
def __init__(self, sigma):
self.sigma = sigma
self.m = None
self.mp = None
self.cov = None
self.alpha = None
self.beta = None
self.x = None
def calculate_kernel(self, x):
n = x.shape[0]
k = [self.kernel(xn, xm) for xn in x for xm in x]
k = np.array(k).reshape(n, n)
k = np.hstack([k, np.ones(n).reshape(-1, 1)])
return k
def kernel(self, xn, xm):
return math.exp(- 0.5 * np.linalg.norm(xn - xm) ** 2 / (self.sigma ** 2))
@staticmethod
def calculate_mu(beta, k, t, sigma):
return beta * np.dot(sigma, np.dot(k.T, t))
@staticmethod
def calculate_cov(a, beta, k):
return np.linalg.inv(np.diag(a) + beta * np.dot(k.T, k))
@staticmethod
def calculate_gamma(a, sigma):
return 1 - a * np.diag(sigma)
def learn(self, x, t, iteration=1):
n = x.shape[0]
a = np.random.uniform(10, 100, n + 1)
beta = np.random.uniform(10, 100, 1)[0]
k = self.calculate_kernel(x)
for c in range(iteration):
cov = self.calculate_cov(a, beta, k)
mu = self.calculate_mu(beta, k, t, cov)
gamma = self.calculate_gamma(a, cov)
mu2 = np.array([a if a != 0 else 1e-16 for a in mu ** 2])
a = gamma / mu2
beta = (n - np.sum(gamma)) / (np.linalg.norm(t - np.dot(k, mu)) ** 2)
self.m = mu
self.cov = cov
self.alpha = a
self.beta = beta
self.x = x
self.mp = np.array([a if math.fabs(a) > 1e-4 else 0.0 for a in self.m])
def predict(self, x):
k = np.array([self.kernel(x, xm) for xm in self.x])
k = np.append(k, 1)
return np.inner(self.m, k)
def predict2(self, x):
k = np.array([self.kernel(x, xm) for xm in self.x])
k = np.append(k, 1)
return np.inner(self.mp, k)
def plot78():
np.random.seed(123)
n = 10
x = np.linspace(0, 1, n)
t = np.sin(2 * np.pi * x) + np.random.normal(0, 0.2, n)
c = 10.0 * n
sigma = 0.2
nu = 0.1
f = NuSvmRegression(nu, c, sigma)
f.learn(x, t)
idx = f.d != 0
axis_x = np.linspace(0, 1, 100)
plt.clf()
plt.plot(axis_x, np.sin(2 * np.pi * axis_x), 'b-')
plt.plot(axis_x, [f.predict(x) for x in axis_x], 'r-')
plt.scatter(x[idx], t[idx], marker='o', c='w', s=80)
plt.scatter(x, t, marker='o', c='g')
plt.savefig('img/f7.8.png')
def plot79():
np.random.seed(123)
n = 10
x = np.linspace(0, 1, n)
t = np.sin(2 * np.pi * x) + np.random.normal(0, 0.2, n)
sigma = 0.2
f = RvmRegression(sigma)
f.learn(x, t, 400)
idx = f.mp[0:n] != 0
axis_x = np.linspace(0, 1, 100)
plt.clf()
plt.plot(axis_x, np.sin(2 * np.pi * axis_x), 'b-')
plt.plot(axis_x, [f.predict(x) for x in axis_x], 'r-')
plt.scatter(x[idx], t[idx], marker='o', c='w', s=80)
plt.scatter(x, t, marker='o', c='g')
plt.savefig('img/f7.9.png')
if __name__ == '__main__':
plot78()
plot79()
print('hello')


から超えた距離
を最小化するように最適化を行う。
-svmでは、
も最適化パラメータとする。このとき、
と
がトレードオフの関係になる。ただし、ラグランジュ未定乗数法の式変形の仮定で消える。
-svmは下記の最小化問題を解く。


