To Do, Doing, Done
因果推論3 操作変数法
統計的因果推論の勉強
- 理論の詳しい話は下記の本を見てください。

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
- 作者: 星野崇宏
- 出版社/メーカー: 岩波書店
- 発売日: 2009/07/29
- メディア: 単行本
- 購入: 29人 クリック: 285回
- この商品を含むブログ (25件) を見る
問題設定
- 目的
- バウチャー制度の効果を評価したい。
- 背景
- くじ引きで当たると、「私立高校へ進学したら授業料が半額になる権利」がもらえる。
- くじ引きは希望者全員が引ける。当たりは40%とする。
- 私立高校、公立高校ともに入学試験はないとする。
- しかし、私立高校の方が質の高い授業を行っているとする。
- 卒業時に、私立・公立高校で統一テストを実施している。
- 状況整理
- 全部で4つのパターンがある
- くじ引き当たり、私立へ進学する
- くじ引き当たり、公立へ進学する
- くじハズれ、私立へ進学する
- くじハズれ、公立へ進学する
- バウチャー制度の評価ポイント
- くじ引きが当たれば、私立へ進学し、外れたら公立へ進学する生徒の卒業時の成績。
- 全部で4つのパターンがある
観察データ作成(ケース1)
- 全体の10%当たりは結果に関係なく必ず公立へ進学する。
- 生徒の20%は裕福で、上記の10%に入った生徒以外はくじ引きの結果に関係なく私立へ進学する。
- 生徒の成績の平均は、y = 600 + 80 * (私立) + 150 * (裕福)
- 観測できない影響を大きくするために、150 * (裕福)とする。
- 標準偏差は50
- 生徒数は1000
- 生成したデータはこんな感じ。
- 生徒が裕福かどうかは不明とする。
lottery private score 0 0 0 605.830138 1 0 0 595.145346 2 0 0 660.159643 3 1 1 676.014558 4 0 0 612.031560 5 0 0 592.204991 6 0 1 704.909145 7 0 0 618.559375 8 0 0 626.251403 9 0 0 536.343088
lottery private score count 1000.00000 1000.000000 1000.000000 mean 0.41700 0.485000 649.887460 std 0.49331 0.500025 72.562223 min 0.00000 0.000000 476.666647 25% 0.00000 0.000000 595.276742 50% 0.00000 0.000000 644.046202 75% 1.00000 1.000000 704.860884 max 1.00000 1.000000 856.068556
簡単な分析(ケース1)
- 単純に私立と公立で平均をとってみる。
- データ生成時のモデル上、差は80程度のはず。
- 他の要素の影響が含まれている。
106.589641791
操作変数法
- 割当
- くじ引きが当たる:
- くじ引きが外れる:
- くじ引きが当たる:
- 操作変数
のとき、私立へ進学する:
のとき、公立へ進学する:
のとき、私立へ進学する:
のとき、公立へ進学する:
- 結果に影響しないので、
仮定する(単調性)
- 私立へ進学するかどうか
- テストの成績
- 独立性
と
は独立
と
は独立
- 推定したいもの
- くじ引きが当たれば私立へ進学するが、外れれば公立へ進学する生徒の成績の差
]
- くじ引きが当たれば私立へ進学するが、外れれば公立へ進学する生徒の成績の差
- 計算する上での問題
- 条件を満たす生徒が誰なのかがわからない。(当たっても私立へ進学しない生徒の存在など。)
- 当然、
か
のどちらかしか観測できていない。
- どう計算するか(詳細な計算は本を見てください)。
- 準備
-E[y|z=0]=E[y_1-y_0|d_1-d_0=0]p(d_1-d_0=1)]
- 以上より
- 最終的にはデータから計算できるものばかりで表される!!
- 準備
- 結果は期待通り80に近い。
81.2776422538
今後の課題
- 結果の検定をどうするのか?
- 入学試験がある場合はどうすればよいか?(選択バイアスが出るよね?)

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
- 作者: 星野崇宏
- 出版社/メーカー: 岩波書店
- 発売日: 2009/07/29
- メディア: 単行本
- 購入: 29人 クリック: 285回
- この商品を含むブログ (25件) を見る
使ったプログラムコード
import numpy as np import pandas as pd def sampling(): n = 1000 score_base = 600 score_private = 80 score_rich = 150 score_sigma = 50 rich_ratio = 0.2 public_ratio = 0.1 winning_ticket_ratio = 0.4 data = pd.DataFrame({ 'rich': np.random.binomial(1, rich_ratio, n), 'lottery': np.random.binomial(1, winning_ticket_ratio, n) }) data['private'] = data.apply(lambda d: 1 if d['rich'] == 1 or d['lottery'] == 1 else 0, axis=1) data['private'] = data['private'] * np.random.binomial(1, 1 - public_ratio, n) data['score'] = score_base + score_private * data['private'] + score_rich * data['rich'] \ + np.random.normal(0, score_sigma, n) return data.drop(['rich'], axis=1) def simple_analysis(data): d0 = data[data['private'] == 0] d1 = data[data.apply(lambda d: d['private'] == 1 and d['lottery'] == 1, axis=1)] print(np.average(d1['score']) - np.average(d0['score'])) def instrumental_variable_method(data): data0 = data[data['lottery'] == 0] data1 = data[data['lottery'] == 1] y0 = np.average(data0['score']) y1 = np.average(data1['score']) d0 = np.average(data0['private']) d1 = np.average(data1['private']) print((y1 - y0) / (d1 - d0)) if __name__ == '__main__': np.random.seed(123) data = sampling() print(data.head(10)) print(data.describe()) simple_analysis(data) instrumental_variable_method(data) print('hello')```
因果推論2 傾向スコア:母集団に偏りがあるときの施策の効果を測る
統計的因果推論の勉強
- 理論の詳しい話は下記の本を見てください。

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
- 作者: 星野崇宏
- 出版社/メーカー: 岩波書店
- 発売日: 2009/07/29
- メディア: 単行本
- 購入: 29人 クリック: 285回
- この商品を含むブログ (25件) を見る
問題
- AとBの2つの学校があり、Aには何か数学の点数が上がるような施策をし、Bには何もしない。
- AとBには、親の学歴の分布が異なる。
- 2つのグループの設定が異なるので、単純には比較できない。
- 親の学歴とかを除いて、施策が効果があったのかを比較したい。
単純に無作為サンプリングできる場合。
- 上記のように異なる特徴をもつ集団があったとしても、AとBの生徒をグチャ混ぜにして、無細工に選んで施策を行った場合、単純に比較できる。
- この場合、施策以外の特徴量を揃えることができるから。
- 例えば、数学の点数は施策に関係なく、親の学歴に依存している場合を考える。

- 赤が施策あり。青が施策なし。
- 縦軸が数学の点数、横軸が親の学歴。
- 赤の平均が49.56。青の平均が49.67。
- 期待通り、今回の施策には効果がないことがわかる。
n = 1000 parent_school_career = np.random.normal(3, 1, n) treated = np.random.binomial(1, 0.5, n) math_score = np.random.normal(50, 10, n) + 10 * (parent_school_career - 3) data = pd.DataFrame({'math': math_score, 'parent': parent_school_career, 'treated': treated}) # plot all sampling data plt.scatter(data['parent'], data['math'], c=data['treated']) plt.show() idx1 = data['treated'] == 1 idx0 = data['treated'] == 0 math0 = data[idx0]['math'] math1 = data[idx1]['math'] print('z=0:', np.average(math0), np.std(math0)) print('z=1:', np.average(math1), np.std(math1))
母集団に偏りがある場合
- Aの親の方がBに比べ、学歴が高いとする。
- Aに施策を行った。

- Aが赤。Bが青。
- 赤の平均が54.74。青の平均が45.49。
- 施策には効果がないのに、平均を単純に比較すると有意に差が出てしまう。
n = 1000 treated = np.random.binomial(1, 0.5, n) parent_school_career = np.random.normal(2.5, 1, n) + treated math_score = np.random.normal(50, 10, n) + 10 * (parent_school_career - 3) data = pd.DataFrame({'math': math_score, 'parent': parent_school_career, 'treated': treated}) # plot all sampling data plt.scatter(data['parent'], data['math'], c=data['treated']) plt.ylabel('math score') plt.xlabel("parent's school career") plt.show() idx1 = data['treated'] == 1 idx0 = data['treated'] == 0 math0 = data[idx0]['math'] math1 = data[idx1]['math'] print('z=0:', np.average(math0), np.std(math0)) print('z=1:', np.average(math1), np.std(math1))
傾向スコアを用いて共変量(親の学歴)の影響をなくす。IPW推定を行う。
- 赤の平均が49.81。青の平均が49.52。
- 共変量の影響がなくなり、期待通り平均の差がなくなった。
def calculate_score(x, alpha): a = np.dot(x, np.array([alpha]).T).flatten() s = 1 / (1 + np.exp(-a)) return s def loglikelihood(x, z, alpha): s = calculate_score(x, alpha) p = z * np.log(s) + (1 - z) * np.log(1 - s) return np.sum(p) def non_random_sampling_ipw(): n = 1000 treated = np.random.binomial(1, 0.5, n) parent_school_career = np.random.normal(2.5, 1, n) + treated math_score = np.random.normal(50, 10, n) + 10 * (parent_school_career - 3) data = pd.DataFrame({'math': math_score, 'parent': parent_school_career, 'treated': treated}) data['const'] = np.ones(n) idx1 = data['treated'] == 1 idx0 = data['treated'] == 0 cons = ( {'type': 'ineq', 'fun': lambda theta: 10 - theta}, {'type': 'ineq', 'fun': lambda theta: theta + 10}, ) alpha = np.random.uniform(0, 1, 2) res = minimize(lambda a: -loglikelihood(data[['parent', 'const']], data['treated'].as_matrix().flatten(), a), alpha, constraints=cons, method="SLSQP") score = calculate_score(data[['parent', 'const']], res.x) w0 = (1 - data['treated']) / (1 - score) w1 = data['treated'] / score n0 = np.sum(w0) n1 = np.sum(w1) y0 = np.sum(w0 * data['math']) / n0 y1 = np.sum(w1 * data['math']) / n1 print(y0) print(y1)
今後の課題
- IPW推定を使ったときの分散はどう求める? どうやって検定を行う?
- 傾向スコアのモデルが適切でないと最終結果がよくない。今回
でなく
としていたときはかなり悪かった。
- 潜在的な共変量があるときはどうすれば?
因果推論1 単純な選択バイアス問題
統計的因果推論の勉強

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
- 作者: 星野崇宏
- 出版社/メーカー: 岩波書店
- 発売日: 2009/07/29
- メディア: 単行本
- 購入: 29人 クリック: 285回
- この商品を含むブログ (25件) を見る
問題
- 大学の入試の結果y1と入学後の成績y2の関係を調べたい。
設定
- 真のモデル
- 入試の平均50、分散40
- 入学後の成績の平均50、分散40
- 2つのテストの相関0.8
- 正規分布に従うと仮定。
- [0, 100]となるように切り捨てる
- 選択バイアス
- 入試の合格点を60とする。
- 当然、入試の60点以下の人の入学後の成績は欠測となる。
を欠測のインディケータとする。この場合、合格のとき
, 不合格のとき
とする。
 - 赤い影になっている部分が欠測データ。
- 赤い影になっている部分が欠測データ。
回帰分析モデルを仮定する。
- モデル
- 最尤推定量
- つまり、
を用いた最小二乗法を行えばよい。
- このときの
の相関は、
parameters: [ 0.63938213 16.73959436] correlation: 0.820560498514
2変量正規分布に従うと仮定する。
- likelihood
- observed data likelihood
- [tex: p(y_1, y_2|\theta) = \prod{i, m_i=1}{p(y(i1), y(i2) | \theta)} \prod{i, m_i=0} p(y(i1) | \theta)]
- つまり、observed data likelihoodを最大化すれば良い。
mu1: 49.73650529 mu2: 48.54009208 sigma1: 10.18582171 sigma2: 7.93686404 rho: 0.820564
Python
import numpy as np import pandas as pd import matplotlib.pyplot as plt import math from scipy.stats import norm, multivariate_normal from scipy.optimize import minimize def negative_log_likelihood(y1, y2, m, m1, m2, s1, s2, rho): mean = np.array([m1, m2]) s12 = rho * s1 * s2 cov = np.array([[s1 * s1, s12], [s12, s2 * s2]]) v = 0.0 for yi1, yi2, mi in zip(y1, y2, m): if mi == 1: v += multivariate_normal.logpdf(np.array([yi1, yi2]), mean=mean, cov=cov) else: v += norm.logpdf(yi1, m1, s1) return -v if __name__ == '__main__': n = 1000 u1 = 50 u2 = 50 v1 = 100 v2 = 50 rho = 0.8 v12 = rho * math.sqrt(v1 * v2) mean = np.array([u1, u2]) cov = np.array([[v1, v12], [v12, v2]]) y = np.random.multivariate_normal(mean, cov, n) data = pd.DataFrame({'y1': y[:, 0], 'y2': y[:, 1]}) data['m'] = data.apply(lambda x: 1 if x['y1'] > 60 else 0, axis=1) data['y2'] = data.apply(lambda x: None if x['m'] == 0 else x['y2'], axis=1) pass_idx = data['m'] == 1 # using regression model coeff = np.polyfit(data[pass_idx]['y1'], data[pass_idx]['y2'], 1) c0 = coeff[0] var_y1 = np.std(data['y1']) ** 2 var_epsilon = np.std(data['y2'] - np.poly1d(coeff)(data['y1'])) ** 2 corr = c0 * var_y1 / (math.sqrt(var_y1) * math.sqrt(c0 ** 2 * var_y1 + var_epsilon)) print('parameters:', coeff) print('correlation:', corr) # using multivariate normal model. cons = ( {'type': 'ineq', 'fun': lambda theta: 0.9999 - theta[4]}, {'type': 'ineq', 'fun': lambda theta: theta[4] + 0.9999}, {'type': 'ineq', 'fun': lambda theta: theta[0:4] - 1}, {'type': 'ineq', 'fun': lambda theta: 100 - theta[0:4]}, ) theta0 = np.array([50, 60, 10, 30, 0.1]) theta = minimize(lambda theta: negative_log_likelihood(data['y1'], data['y2'], data['m'], theta[0], theta[1], theta[2], theta[3], theta[4]), theta0, constraints=cons, method="SLSQP") print(theta) axis_x = np.linspace(0, 100, 101) plt.scatter(y[:, 0], y[:, 1]) plt.fill_betweenx((-10, 110), 60, facecolor='r', alpha=0.2) plt.xlim(0, 100) plt.ylim(0, 100) plt.plot(axis_x, np.poly1d(coeff)(axis_x)) plt.xlabel('y1') plt.ylabel('y2') plt.show()
PRML 7. Sparse Kernel Machines (Regression with SVM and RVM)
- PRML本の7章でサポートベクターマシン等を使った回帰。
- 機械学習等は勉強中で、内容に誤りがある可能性が十分にあります。指摘していただけると嬉しいです

- 作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
- 出版社/メーカー: 丸善出版
- 発売日: 2012/04/05
- メディア: 単行本(ソフトカバー)
- 購入: 6人 クリック: 33回
- この商品を含むブログ (18件) を見る
概要
- しきい値
から超えた距離
を最小化するように最適化を行う。
- svmではしきい値はgivenとするが、
-svmでは、
も最適化パラメータとする。このとき、
と
がトレードオフの関係になる。ただし、ラグランジュ未定乗数法の式変形の仮定で消える。
-svmは下記の最小化問題を解く。
- Relevance Vector Machine (RVM)はベイジアンなkernel method.
- 3章と同様に、事前分布のパラメータをiterativeに解く。
- SVMと比べ、予測時に使用する入力データの数が少なくなりやすい。
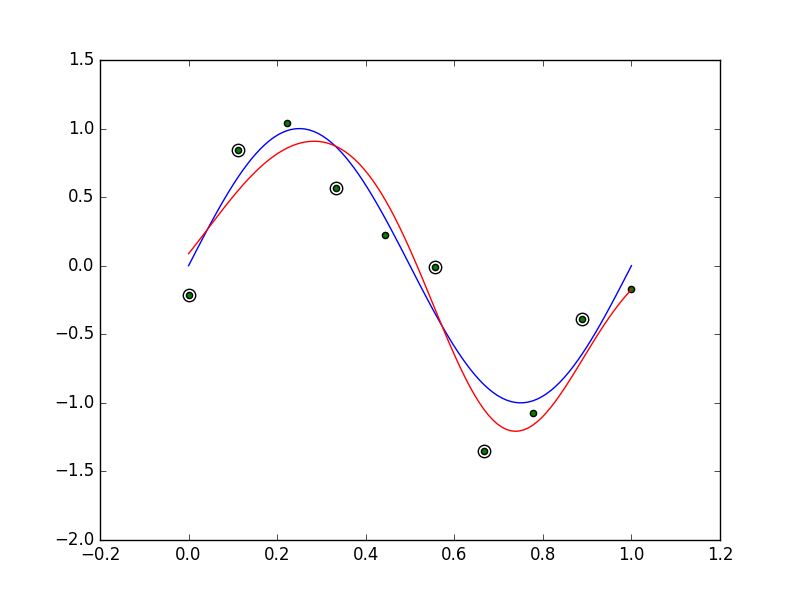
図7.8の再現
図7.9の再現
Python
- Python初心者なので、まだまだ汚いです。そのうち修正する。
import numpy as np import matplotlib.pyplot as plt from scipy.optimize import minimize import math class NuSvmRegression: def __init__(self, nu, c, sigma): self.nu = nu self.c = c self.sigma = sigma self.x = None self.t = None self.b = None self.d = None def kernel(self, xn, xm): return math.exp(- 0.5 * np.linalg.norm(xn - xm) ** 2 / (self.sigma ** 2)) def __call__(self, a): n = a.shape[0] // 2 a0, a1 = a[0:n], a[n:2 * n] d = (a0 - a1).flatten() k = np.array([self.kernel(xn, xm) for xn in self.x for xm in self.x]).reshape(n, n) v = - np.sum(d * self.t) for i in range(n): for j in range(n): v += 0.5 * d[i] * d[j] * k[i][j] return v def learn(self, x, t): self.x = x self.t = t n = x.shape[0] initial_a = np.random.uniform(0, 1, n * 2) cons = ({'type': 'ineq', 'fun': lambda a: a}, {'type': 'ineq', 'fun': lambda a: self.c / n - a}, {'type': 'ineq', 'fun': lambda a: self.nu * self.c - np.sum(a[0:n] + a[n:2 * n])}, {'type': 'eq', 'fun': lambda a: np.sum(a[0:n] - a[n:2 * n])}) res = minimize(self, initial_a, method='SLSQP', tol=1e-6, constraints=cons) a = res.x a0, a1 = a[0:n], a[n:2 * n] d = (a0 - a1) d = np.array([d0 if math.fabs(d0) > 1e-4 else 0 for d0 in d]).reshape(1, -1) k = np.array([self.kernel(xn, xm) for xn in self.x for xm in self.x]).reshape(n, n) self.b = np.average(t - np.dot(d, k)) self.d = d.flatten() return res.x def predict(self, x): n = self.t.shape[0] k = np.array([self.kernel(x, xm) for xm in self.x]) return np.sum(self.d * k) + self.b class RvmRegression: def __init__(self, sigma): self.sigma = sigma self.m = None self.mp = None self.cov = None self.alpha = None self.beta = None self.x = None def calculate_kernel(self, x): n = x.shape[0] k = [self.kernel(xn, xm) for xn in x for xm in x] k = np.array(k).reshape(n, n) k = np.hstack([k, np.ones(n).reshape(-1, 1)]) return k def kernel(self, xn, xm): return math.exp(- 0.5 * np.linalg.norm(xn - xm) ** 2 / (self.sigma ** 2)) @staticmethod def calculate_mu(beta, k, t, sigma): return beta * np.dot(sigma, np.dot(k.T, t)) @staticmethod def calculate_cov(a, beta, k): return np.linalg.inv(np.diag(a) + beta * np.dot(k.T, k)) @staticmethod def calculate_gamma(a, sigma): return 1 - a * np.diag(sigma) def learn(self, x, t, iteration=1): n = x.shape[0] a = np.random.uniform(10, 100, n + 1) beta = np.random.uniform(10, 100, 1)[0] k = self.calculate_kernel(x) for c in range(iteration): cov = self.calculate_cov(a, beta, k) mu = self.calculate_mu(beta, k, t, cov) gamma = self.calculate_gamma(a, cov) mu2 = np.array([a if a != 0 else 1e-16 for a in mu ** 2]) a = gamma / mu2 beta = (n - np.sum(gamma)) / (np.linalg.norm(t - np.dot(k, mu)) ** 2) self.m = mu self.cov = cov self.alpha = a self.beta = beta self.x = x self.mp = np.array([a if math.fabs(a) > 1e-4 else 0.0 for a in self.m]) def predict(self, x): k = np.array([self.kernel(x, xm) for xm in self.x]) k = np.append(k, 1) return np.inner(self.m, k) def predict2(self, x): k = np.array([self.kernel(x, xm) for xm in self.x]) k = np.append(k, 1) return np.inner(self.mp, k) def plot78(): np.random.seed(123) n = 10 x = np.linspace(0, 1, n) t = np.sin(2 * np.pi * x) + np.random.normal(0, 0.2, n) c = 10.0 * n sigma = 0.2 nu = 0.1 f = NuSvmRegression(nu, c, sigma) f.learn(x, t) idx = f.d != 0 axis_x = np.linspace(0, 1, 100) plt.clf() plt.plot(axis_x, np.sin(2 * np.pi * axis_x), 'b-') plt.plot(axis_x, [f.predict(x) for x in axis_x], 'r-') plt.scatter(x[idx], t[idx], marker='o', c='w', s=80) plt.scatter(x, t, marker='o', c='g') plt.savefig('img/f7.8.png') def plot79(): np.random.seed(123) n = 10 x = np.linspace(0, 1, n) t = np.sin(2 * np.pi * x) + np.random.normal(0, 0.2, n) sigma = 0.2 f = RvmRegression(sigma) f.learn(x, t, 400) idx = f.mp[0:n] != 0 axis_x = np.linspace(0, 1, 100) plt.clf() plt.plot(axis_x, np.sin(2 * np.pi * axis_x), 'b-') plt.plot(axis_x, [f.predict(x) for x in axis_x], 'r-') plt.scatter(x[idx], t[idx], marker='o', c='w', s=80) plt.scatter(x, t, marker='o', c='g') plt.savefig('img/f7.9.png') if __name__ == '__main__': plot78() plot79() print('hello')

- 作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
- 出版社/メーカー: 丸善出版
- 発売日: 2012/04/05
- メディア: 単行本(ソフトカバー)
- 購入: 6人 クリック: 33回
- この商品を含むブログ (18件) を見る
PRML 7. Sparse Kernel Machines (Classification with SVM)
- PRML本の7章でサポートベクターマシンを使った分類アルゴリズム。
- 機械学習等は勉強中で、内容に誤りがある可能性が十分にあります。指摘していただけると嬉しいです

- 作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
- 出版社/メーカー: 丸善出版
- 発売日: 2012/04/05
- メディア: 単行本(ソフトカバー)
- 購入: 6人 クリック: 33回
- この商品を含むブログ (18件) を見る
概要
- 分類の境界線から一番違い要素との距離を最大化するように最適化を行う。
- 2クラスの分類を扱うが、多クラスへの応用はストレートにできる。
- 最大化問題をラグランジュ未定乗数法を用いて双対問題を作り、双対問題を解く。
- 予測時に一部の学習データのみを用いる。それらをサポートベクターと呼ぶ。
- 式変形は単純なので、メモなし。
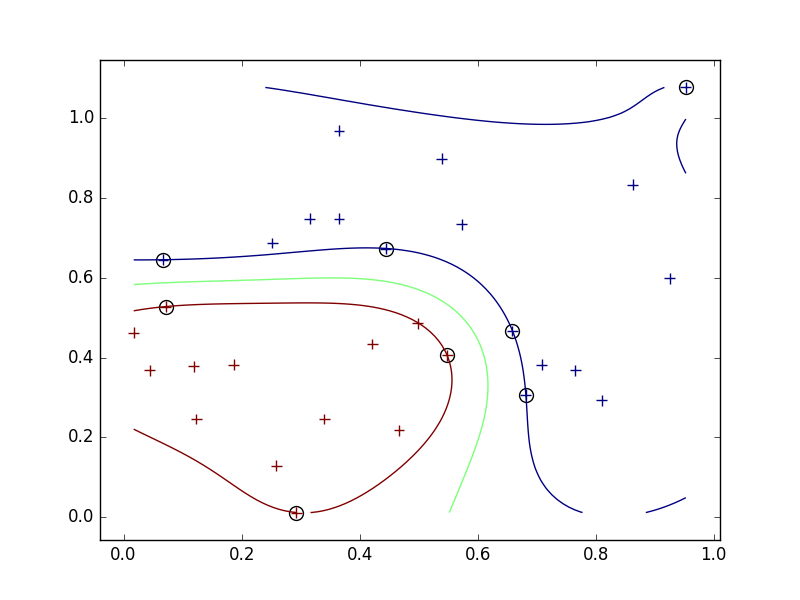
図7.2の再現
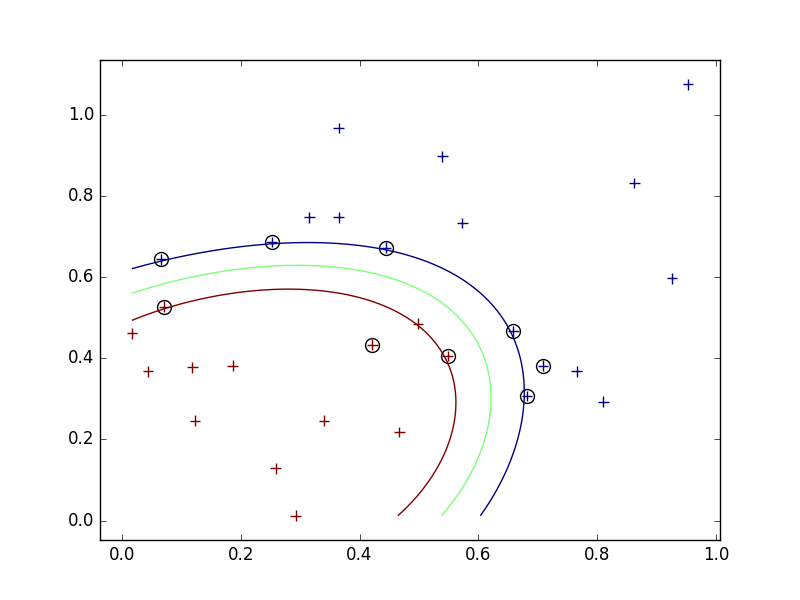
sigmaによる結果への影響について。
- 今回、Gaussianカーネルを使っているので、sigmaは各学習用データがその周りに与える影響の大きさを表している。
- 小さすぎるとサブセットの周りを囲むような境界線になってしまい、汎用性がさがる。
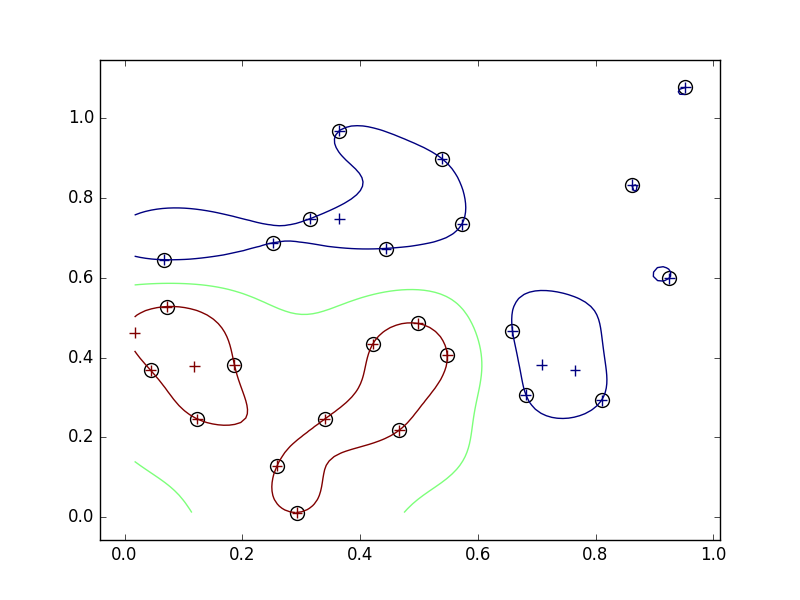
- 逆に大きくするとデータから遠いところが大雑把になりそう。
外れ値
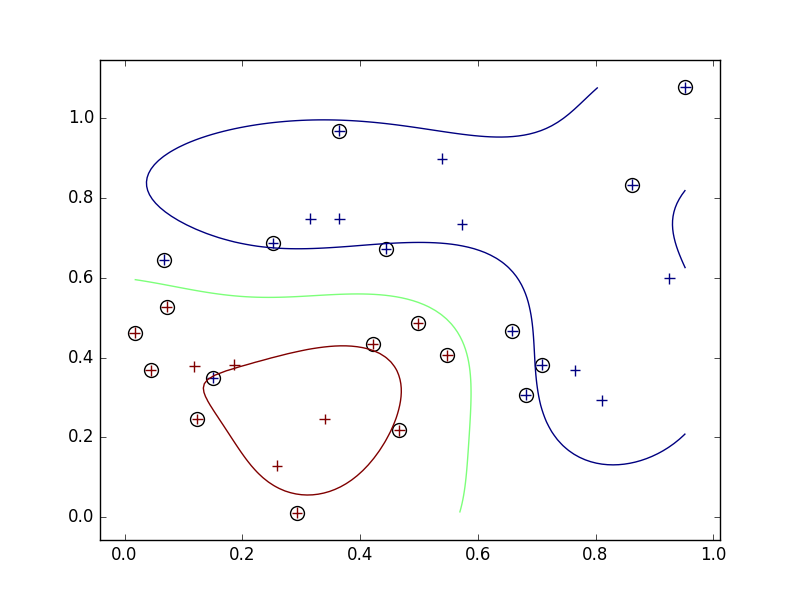
- ナイーブに最大化問題を解くと、外れ値に対応できない。
- アルゴリズム上、すべての学習データを正しく分類する。汎用性が低くなる可能性がある。
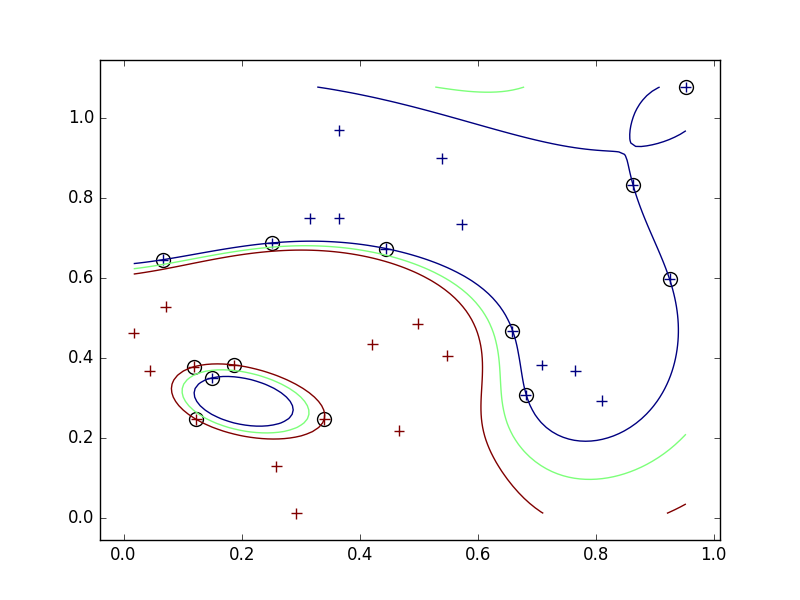
- そこで、スラック変数を導入して、誤って分類させることを許し、そのかわりにペナルティを与えるようにする。
- スラック変数導入前は、左下の青い一点を囲むような境界ができていたが、導入後は左下の青い点は間違った分類(赤)になったままになった。
Python
import numpy as np import matplotlib.pyplot as plt from scipy.optimize import minimize import math class DualRepresentation: def __init__(self, x, t, sigma, c): self.x = x self.t = t.flatten() self.sigma = sigma self.a = None self.b = 0 self.c = c def kernel(self, xn, xm): return math.exp(- 0.5 * np.linalg.norm(xn - xm) ** 2 / (self.sigma ** 2)) def __call__(self, input): n = self.t.shape[0] a = np.array(input).flatten() k = np.array([self.kernel(xn, xm) for xn in self.x for xm in self.x]).reshape(n, n) v = np.sum(a) for i in range(n): for j in range(n): v -= 0.5 * a[i] * a[j] * self.t[i] * self.t[j] * k[i][j] return -v def set(self, a): n = self.t.shape[0] self.a = a idx = np.where(a != 0) ns = idx[0].shape[0] k = np.array([self.kernel(xn, xm) for xn in self.x for xm in self.x]).reshape(n, n) b = 0.0 for i in idx[0]: b += self.t[i] for j in idx[0]: b -= a[j] * self.t[j] * k[i][j] self.b = b / ns def learn(self): n = self.t.shape[0] a0 = np.random.uniform(0, 1, n) cons = ({'type': 'ineq', 'fun': lambda a: a}, {'type': 'eq', 'fun': lambda a: np.sum(self.t * a) - 1}, {'type': 'ineq', 'fun': lambda a: self.c - a}) res = minimize(self, a0, method='SLSQP', tol=1e-6, constraints=cons) a = np.array([x if x > 1e-12 else 0.0 for x in res.x]) self.set(a) return a def predict(self, x): n = self.t.shape[0] k = np.array([self.kernel(x, xm) for xm in self.x]) return np.sum(self.a * self.t * k) + self.b def plot72(x, t, sigma, c=1e+16, do_save=None): n = data.shape[0] f = DualRepresentation(data[:, 0:2], t, sigma, c) a = f.learn() n_plot = 100 axis_x0 = np.linspace(np.min(x[:, 0]), np.max(x[:, 0]), n_plot) axis_x1 = np.linspace(np.min(x[:, 1]), np.max(x[:, 1]), n_plot) boundary = np.array([f.predict(np.array([x0, x1])) for x0 in axis_x0 for x1 in axis_x1]).reshape(n_plot, n_plot) idx = np.where(a != 0.0) plt.clf() plt.scatter(x[idx, 0], x[idx, 1], c='w', marker='o', s=100) plt.scatter(x[:, 0], x[:, 1], c=t, marker='+', s=60) plt.contour(axis_x0, axis_x1, boundary.T, np.array([-1, 0, 1])) if do_save is None: plt.show() else: plt.savefig(do_save) if __name__ == '__main__': data = np.genfromtxt('dataset/classification_7_2.csv', delimiter=',').astype(np.float32) plot72(x=data[:, 0:2], t=data[:, 2], sigma=0.1, do_save='img/f7.2_0.1.png') plot72(x=data[:, 0:2], t=data[:, 2], sigma=0.2, do_save='img/f7.2_0.2.png') plot72(x=data[:, 0:2], t=data[:, 2], sigma=0.5, do_save='img/f7.2_0.5.png') data = np.vstack([data, np.array([[0.15, 0.35, -1]])]) plot72(x=data[:, 0:2], t=data[:, 2], sigma=0.2, do_save='img/f7.2_0.2_outlier.png') plot72(x=data[:, 0:2], t=data[:, 2], sigma=0.2, c=1, do_save='img/f7.2_0.2_outlier_slack.png')

- 作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
- 出版社/メーカー: 丸善出版
- 発売日: 2012/04/05
- メディア: 単行本(ソフトカバー)
- 購入: 6人 クリック: 33回
- この商品を含むブログ (18件) を見る
2017年の目標
今年は去年より勉強に使える時間が増えそうなので、がっつり勉強したい。転職時に1ヶ月程度間を入れてじっくりと学べるかな。
(1) 機械学習を学ぶ
クオンツからデータアナリストに変わろうと思う。統計等は学部時代に勉強していたけど、機械学習はさらっとライブラリの使い方解説本を読んだ程度。プロとして最低限のレベルに達したい。
(2) 分析経験を積む
「いかに使うか」が重要なので、経験値を積みたい。業務で使用するだろうけど、幅広く色々分析したいので、ちょっと意識してデータを分析していく。
- 1ヶ月に1つ程度、データを分析して、その過程をブログにアップする。
(3) その他
教養がないので、世界史や生物学の本を読もうと思う。何がいいのかわからないけど、本やで適当に探そう。あと、インプットだけでなくアウトプットをしっかりと出していきたい。
- 1ヶ月に1冊読んで、感想をブログに書く。
- ブログを続ける
変化のある年に
10年近く勉強してきたクオンツ業界から離れることを決意したので、節目の年になる。新しい分野でしっかりと結果を出していきたい。